代数图论2：代数结构

自同构 isomorphism

定义

An isomorphism from a graph $X$ to itself is called an automorphism of $X$. An automorphism is therefore a permutation of the vertices of $X$ that maps edges to edges and nonedges to nonedges.

所谓自同构，就是自己到自己的一个同构。

至于为什么要考虑自同构，是因为我们需要利用这里天然形成的一个群结构。也就是所谓“代数”。

自同构群 isomorphism group

The set of all automorphisms of $X$ forms a group, which is called the automorphism group of $X$ and denoted by $\mathrm{Aut}( X)$.

价态 Valency

The valency of a vertex xis the number of neighbours of x, and the maximum and minimum valency of a graph $X$ are the maximum and minimum values of the valencies of any vertex of $X$.

价态，大致是刻画一个点与其他点连通的程度的量。

下面有一个优美的等式，也比较好证明，主要考虑每个边都连接了两个顶点

Fubini’s throrem

\(2|E(X)| = \sum_{v \in V(X)} (\text{valency of }v)\)

Lemma 1.3.1

If $x$ is a vertex of the graph $X$ and g is an automorphism of $X$, then the vertex $y = x^g$ has. the same valency as $x$.

这说明自同构大致保持顶点与周围连接不变，该连几条边还得要连几条边。

Lemma 1.3.2

If $x$ and $y$ are vertices of $X$ and $g \in Aut(X)$, then $d(x,y) = d(x^g,y^g)$.

事实上，这表明了一些自同构的“刚性”。

补图

The complement $X$ of a graph $X$ has the same vertex set as $X$, where vertices $x$ and $y$ are adjacent in $X$ if and only if they are not adjacent in $X$ (se Figure 1.5).

简单来说，补图是将边集相对于同顶点的完全图的边集取补。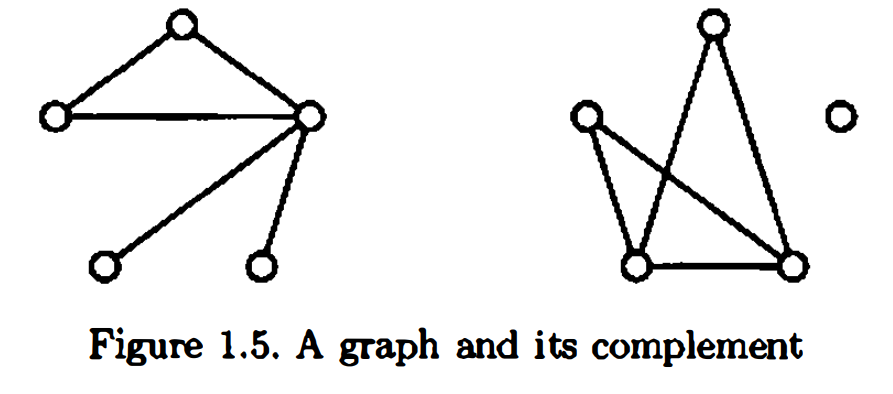

Lemma 1.3.3

The automorphism group of a graph is equal to the automorphism group of its CQmplement.

只需要证明 一个图的自同构就是它的补图的自同构。

同态 homomorphism

怎么这也有homo啊

Let $X$ and $Y$ be graphs. A mapping $f$ from $V(X)$ to $V(Y)$ is a homomorphism if $f(x)$ and $f (y)$ are adjacent in $Y$ whenever $x$ and $y$ are adjacent in $X$. (When $X$ and $Y$ have no loops, which is our usual case, this definition implies that if $x \sim y$, then $f(x) \not = f (y)$.)

事实上，同态完成的是一个折叠的感觉，而非压缩，因为它要求保持毗邻的性质，这意味着，它不能将相邻的两个点映入同一个点。

我们可以验证，两个同态的复合，依旧是一个同态。 由此，其实我们就已经定义了一个在有限图上的范畴category。只是可惜，这个同态不是additive（加性范畴）。

一些例子

Example 1

可以存在的同态 任意大的二部图，都存在一个到$K_2$的满同态 如果$|X|=n$，那么存在一个满同态$f:X \to K_n$ 不存在同态$f:K_3 \to K_2$，使得f是满的

问题

关于一个有限图，我们会好奇它所能映入的最小的kn是怎么样的。（这里的引入使用的是同态） 那么，这就与着色数有关。也就是说，给每个顶点染色，要求相邻的顶点不同色。而所需最少的颜色数，我们称之为着色数(chromatic number)。

而这与同态息息相关

Lemma 1.4.1

The chromatic number of a graph $X$ is the least integer $r$ such that there is a homomorphism from $X$ to $K_r$ .

proof. 大致想法如下， 若存在一个同态$f:X \to K_n$，那么可以将映射到同一个点的的点染成同一个颜色。因此有$n \ge r$. 另一方面，如果有一个用了r种颜色的合法染色方式，那么我们可以将同一种颜色的点映射到$K_r$的同一个点，不同颜色就映射到不同点。因为相邻的点之间颜色不同，所以会映射到$K_r$中的不同点，因此依旧存在一个边连接他们的像。因此这样定义的映射是个同态。

二部图 bipartite

A graph $X$ is called bipartite if its vertex set can be partitioned into two parts $V_1$ and $V_2$ such that every edge has one end in $V_1$ and one in $V_2$•

Theorem 树的边

对于一个树$X$， \(|E(X)| = |V(X)|-1\)

Lemma 树的叶

每个拥有至少两个顶点的树，都有一个价态为1的顶点。

Theorem 对二部图的局部刻画

$X$ is bipartite iff $X$ has an odd cycles.

proof. 简单总结一下想法， 左推右比较简单，只需要对这个环逐个染色即可导出矛盾。

右推左，不妨假设这张图是连通的（毕竟不同的两个连通分支之间几乎没有什么关系可言）。

再次强调，这里的结果都是针对简单图而言，因为如果存在点到自己的loop，那么我们 的论述就会出问题了。

收缩

A retraction is a homomorphism f from a graph X to a subgraph Y of itself such that the restriction $J

Y$ off to V(Y) is the identity map. If there is a retraction from X to a subgraph Y, then we say that Y is a retract of X. If the graph X has a clique of size $k = \chi(X)$, then any $k$-colouring of X determines a retraction onto the clique.

Lemma

如果$Y$是$X$的一个收缩核(retract)，那么

• $Y$ is a induced subgraph
• $\forall a,b \in V(Y), d_Y(a,b) = d_X(a,b)$

第一个是比较平凡的。 第二个则是依赖收缩映射的同态性质，这意味着在$X$中连接$a,b$一条路径，都会对应一条同样长度的在$Y$中的路径。

同态幺半群

A homomorphism from a graph $X$ to itself is called an endomorphism, and the set of all endomorphisms of $X$ is the endomorphism monoid of $X$.