代数数论 类数有限
Published:
Introduction
Definition A Dedekind domain is a noetherian integrally closed integral domain in which any nonzero prime ideal is maximal.
Basically a Dedekind domain should be thought as a smooth curve. (挖坑，回头再来整理，这里的核心思想正是代数几何在代数数论中的应用)
If $K$ is a number field, then $\mathcal O_K$ is a Dedekind domain. Same is true for any localization of $\mathcal O_K$. PID $\Rightarrow$ Dedekind domain.
Theorem Every nonzero ideal $\mathfrak{a}$ in a Dedekind domain $R$ can be written as a product of maximal ideals $\mathfrak{a} = \mathfrak{p}_1 \dots \mathfrak{p}_n$ unique up to permutation.
proof. you can find it in Algebraic Number Theory.
Definition (fractional ideal) Let R be a Dedeking domain and $K = \text{Frac}(R)$. A fractional ideal of $R$ is an $R$-submodule $0 \not = M ⊂ K$ such that $aM ⊂ R$ for some nonzero $a \in R$
For any nonzero $\alpha \in K^\times, (\alpha) = \alpha R$ is a fractional ideal. Such fractional ideals are called principal.
Theorem The set of fractional ideals of a Dedekind domain $R$ form an abelian group under products of ideals. The unit element is $R$ and the inverse of a fractional ideal $\mathfrak{a}$ is $\mathfrak{a}^{−1} := {x \in K = \mathrm{Frac}(R), x \mathfrak{a} ⊂ R}$. $\mathfrak{a}^{−1}$ is also a fraction ideal of $R$.
proof. you can find it in Algebraic Number Theory.
既然戴德金环天然送给我们一个群的结构，那么很自然的一个问题就是查看这个群结构是否在我们熟悉的$K$的乘法群结构上提供了更多的信息。 Denote by $J_R$ the group of fractional ideals and $P_R ⊂ J_R$ the subgroup of principal fractional ideals.
Definition (ideal class group) The ideal class group of $R$ is $\mathrm{Cl}R := J_R/P_R$. For a number field $K$, we denote $\mathrm{Cl}_K := \mathrm{Cl}{\mathcal O_K}$ and call it the ideal class group of $K$.
We have an exact sequence \(1 \to R^\times \to K^\times \to J_R \to \mathrm{Cl}_R \to 1\) The ideal class group precisely measures the failure of unique factorization of elements. 事实上，$\mathrm{Cl}_R$ 给我们提供了更多的信息。
property of $\mathrm{Cl}_R$
在继续我们的旅途之前，先看一看这个新出现的$\mathrm{Cl}_R$的性质。
Proposition For a Dedekind domain R, the following are equivalent (1) $\mathrm{Cl}_R = 1$; (2) $R$ is a PID; (3) $R$ is a UFD; (4) Every prime ideal of $R$ is principal.
proof. (4) $\Rightarrow$ (1), the condition is actually a disguised that $J_R = P_R$, then it is clear. (1) $\Rightarrow$ (2), obviously by definition. (2) $\Rightarrow$ (3), obviously by Abstract algebra. (3) $\Rightarrow$ (4), using property of Dedekind domain, every nonzero prime ideal is maximal ideal. Let $p$ be a nonzero prime ideal in a Dedekind domain $A$ that is also a UFD, let $a \in p$ nonzero, and let $a = p_1 \cdots p_n$ be the unique factorization of a into irreducible elements. Now $\mathfrak{p}$ contains and therefore divides $(a) = (p_1)\cdots(p_n)$, so p divides (and therefore contains) some $(p_i)$, which is necessarily a prime ideal (in a UFD, irreducible elements generate prime ideals). But $A$ has dimension one, so we must have $\mathfrak{p} = (p_i)$
还有一个我们暂时不会去证明的定理
Theorem For any ideal class $C \in \mathrm{Cl}_K$, the set of prime ideals in $C$ has Dirichlet density $\frac{1}{|\mathrm{Cl}_K|}$ .
不过，要理解什么是 Dirichlet density ，我们需要引入一些关于 zeta function 和 L-function 的知识。（挖坑，回头整理）
Norm
为了度量清楚一个域的类数，我们接着引入一些相对比较直接的“测量”数域的工具。
norm
大致思想是将 $L$ 视作 $F$ 线性空间，以展开数域那些挤在一起的代数结构（这个思想也会在后面得到体现）
Definition norm Let $L/F$ be a finite field extension. Let $\mu_\alpha$ be the $K$-linear endomorphism of $L$ defined by multiplication by $\alpha$. \(N_{L/F}(\alpha):=\det(\mu_\alpha) = \prod_{\tau \in \mathrm{Hom}(L,\overline{F})} \tau(\alpha)\)
norm 度量了 这个数在乘法的过程中让数域膨胀了多少。
But, as we all know, the element is not always work on the ring. In this way, we need to construct a more general norm on ideals of the ring. To do this, we consider the $\mathcal O_K$ as the $\mathbb Z$-module.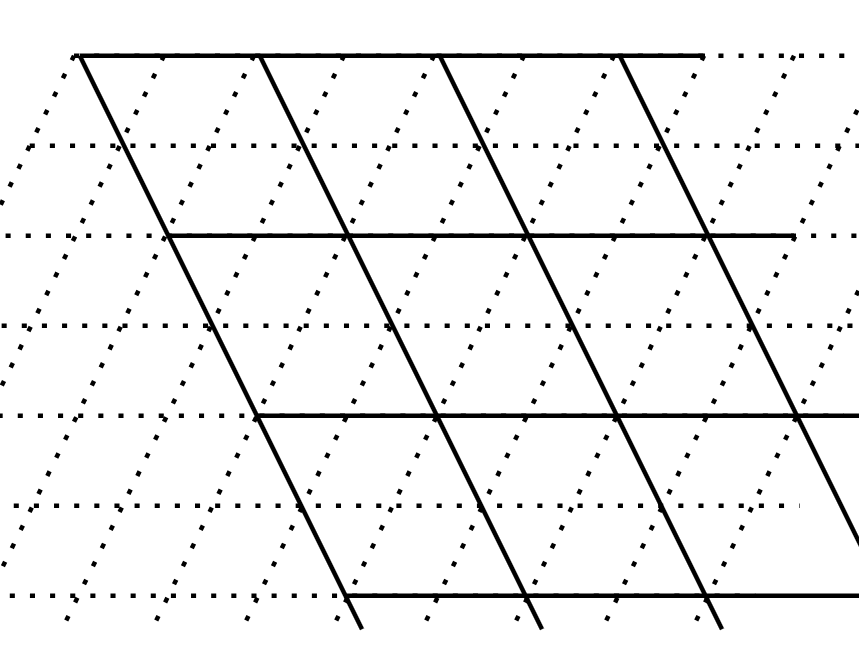 
then, the det of a grid is equal to the number of elements of $|M/\Lambda|$.
absolute norm
Def. (absolute) norm For any nonzero ideal $\mathfrak a \subset \mathcal O_K$, define its (absolute) norm to be the index \(N \mathfrak a = |\mathcal O_K / \mathfrak a | = [\mathcal O_K : \mathfrak a]\)
Prop.
- this number is finite.
For a nonzero $\alpha \in \mathcal O_K$, $N(\alpha) = \mathcal O_K / \alpha \mathcal O_K = N_{K/\mathbb Q} \alpha $ - $N(\mathfrak{a}\mathfrak{b}) = N(\mathfrak{a}) N(\mathfrak{b})$
- For a nonzero prime ideal $\mathfrak{p} \subset \mathcal O_K$ with $\mathfrak{p} \cap \mathbb Z = p \mathbb Z$, we have $N \mathfrak{p} = p^{f(\mathfrak{p})}$ which $f(\mathfrak{p})$ is the inertia degree of $\mathfrak{p}$ over $p \mathbb Z$
proof 1) Since $\mathfrak a$ and $\mathcal O_K$ are free abelian groups(as an $\mathbb Z$-module) of the same rank, this number is finite. 2) check as difinition. 3) verify by the definition. 4) Since $\kappa(\mathfrak{p}) = \mathcal O_K / \mathfrak{p}$ is the finite extension of $\mathbb F_p$ of degree $f(\mathfrak{p})$, we have $N\mathfrak{p} = p^{f(\mathfrak{p})}$.
$\mathrm{Cl}_K$ is finite
Theorem For a number field $K$, the ideal class group $\mathrm{Cl}_K$ is finite.
To prove the theorem, we need a lemma.
Lemma For any constant $C > 0$, there are only finitely many nonzero ideals $\mathfrak a \subset \mathcal O_K$ with $N \mathfrak a \le C$.
proof of lemma. (can be skipped) For a fix $C$, ${p \in \mathbb Z: p < C}$ is finite set. For any $p \in \mathbb Z$, the prime ideal $\mathfrak{p} \subset \mathcal O_K$ with $\mathfrak{p} \cap \mathbb Z = p \mathbb Z$ is finite. For any ideal $\mathfrak{a} \subset \mathcal O_K$, we can write them as the product of prime ideals $\mathfrak{a} = \mathfrak{p}_1^{r_1} \cdots \mathfrak{p}_s^{r_s}$, then $N\mathfrak{a} = p_1^{r_1 f(\mathfrak{p}_1)} \cdots p_s^{r_s f(\mathfrak{p}_s)} \ge p_1^{r_1} \cdots p_s^{r_s}$. Thus, ${\mathfrak{a}:N\mathfrak{a} < C} \subset {\mathfrak{a} = \mathfrak{p}_1^{r_1} \cdots \mathfrak{p}_s^{r_s}: p_1^{r_1} \cdots p_s^{r_s} < C}$ is a finite set.
first proof of theorem. Choose a $\mathbb Z$-basis $\omega_1,\dots,\omega_n$ of $\mathcal O_K$. For a class $[\mathfrak{c}] \in \mathrm{CL}_K$, we choose a fractional ideal in $C$, which have the form $\mathfrak b^{-1} \subset [\mathfrak{c}]$ for some $\mathfrak b \subset \mathcal O_K$. (we always can choose such fraction ideal, because we can multiply element of $K$ without change the class.)
Consider the finite set \(S=\{\alpha = \sum_{i=1}^nm_i \omega_i \in \mathcal O_K : m_i \in \mathbb Z, 0\le m_i < (N \mathfrak b)^{\frac 1 n} + 1\}\) whose cardinality satisfies $|S| > N \mathfrak{b} = [\mathcal O_K : \mathfrak{b}]$. By pigeonhole principle, there exist two different element $\alpha, \beta \in S$ such that $\alpha - \beta \in \mathfrak{b}$. Let $\mathfrak{a} = (\alpha - \beta) \mathfrak{b}^{-1} \in [\mathfrak c]$. Write $\alpha - \beta = \sum_{i=1}^n r_i \omega_i$ with $|r_i| <(N \mathfrak b)^{\frac 1 n} + 1$ . Then, we have \(\begin{eqnarray} |N_{K/\mathbb Q}(\alpha - \beta)| & = & \prod_{j = 1}^n\left|\sum_{i = 1}^n r_i \tau_j(\omega_i)\right|\\ &<& \prod_{j = 1}^n \left[ \left( (N\mathfrak b)^{\frac 1 n} + 1 \right) \sum_{i = 1}^n \left| \tau_j(\omega_i)\right| \right]\\ &\le& C \left( (N\mathfrak b)^{\frac 1 n} + 1 \right) \end{eqnarray}\) where $C=\prod_{j = 1}^n \left(\sum_{i = 1}^n \left| \tau_j(\omega_i)\right|\right)$ is a constant independent of $\mathfrak a$. Then we get\(N \mathfrak a = |N_{K/\mathbb Q} (\alpha - \beta)|(N \mathfrak b)^{-1} < C(1+(N \mathfrak b)^{\frac 1 n})^n\) Since we can replace the $\mathfrak b$ by $x\mathfrak b$ for some $x \in \mathcal O_ K$, then we can find $\mathfrak a \in [\mathfrak c]$ such that \(N\mathfrak a < 2C\)
Using the lemma, we conclude that $\mathrm{Cl}_K$ is finite.
a better bounded
接下来，如果我们想的话，还可以用Minkowski bound 来得到一个更好的上界。 这里的主要想法还是将“压缩在一条直线上”密密麻麻的“代数整数”分离出来，就是一种展开的感觉。
因为$K$ 是有限维的 $\mathbb Q$-module 所以 $\mathcal O_K$ 是有限维的 $\mathbb Z$-module。
discriminant of number field
Definition trace Let $L/F$ be a finite field extension. Let $\mu_\alpha$ be the $K$-linear endomorphism of $L$ defined by multiplication by $\alpha$. \(\mathrm{Tr}_{L/F}(\alpha):=\mathrm{Tr}(\mu_\alpha :L \to L)\)
trace pairing
Definition The trace pairing on $L$ is the symmetric $F$-bilinear form $L \times L \to F$ defined by $(\alpha, \beta) \mapsto \mathrm{Tr}_{L/K} (\alpha \beta)$ for all $\alpha, \beta \in L$.
discriminant
Definition Let $n = [L : K]$. The discriminant of $n$-elements $x_1,\dots , x_n \in L$ is defined by \(d(x_1, \dots , x_n) := (x_1 \wedge \dots \wedge x_n, x_1 \wedge \dots \wedge x_n) = \det(\mathrm{Tr}_{L/K} (x_i x_j))\)
The trace pairing is nondegenerate if and only if the discriminant is not identically zero, in which case $d(x_1, \dots , x_n) \not = 0$ if and only if $x_1, \dots , x_n$ form an $F$ basis of $L$.
Definition The discriminant of a lattice $M \subset K$ is the integer $d(M ) := d(\omega_1, \dots, \omega_n)$ where $\omega_1, \dots , \omega_n$ is a $\mathbb Z$-basis of $M$ .
各位可以自行验证，这个定义并不依赖于这组基的选取。 而这里需要的一个观察是，$\mathcal O_K$ 是 $K$ 里的一个 lattice
Definition The discriminant of the number field $K$ is the discriminant of the lattice $\mathcal O_K$. We denote it by $d_K := d(\mathcal O_K )$
由此，可以利用这个定义来“度量”这个数域里面的整数有多散
Minkowski bound
Let $K_{\mathbb R} := K \otimes_{\mathbb Q}\mathbb R$. $\forall \tau \in \mathrm{Hom}_{\mathbb Q}(K, \mathbb C)$, we call real embedding if $\tau = \overline{\tau}$ ; imaginary embedding otherwise. ${\rho_i : K \hookrightarrow \mathbb R, 1 \le j \le r_1}$ all the real embedding ${\sigma_i, \overline{\sigma_i} : K \hookrightarrow \mathbb C, 1 \le j \le r_2}$ all the imaginary imbedding Then, we have $n = r_1 + 2r_2$, and a $\mathbb R$-algebra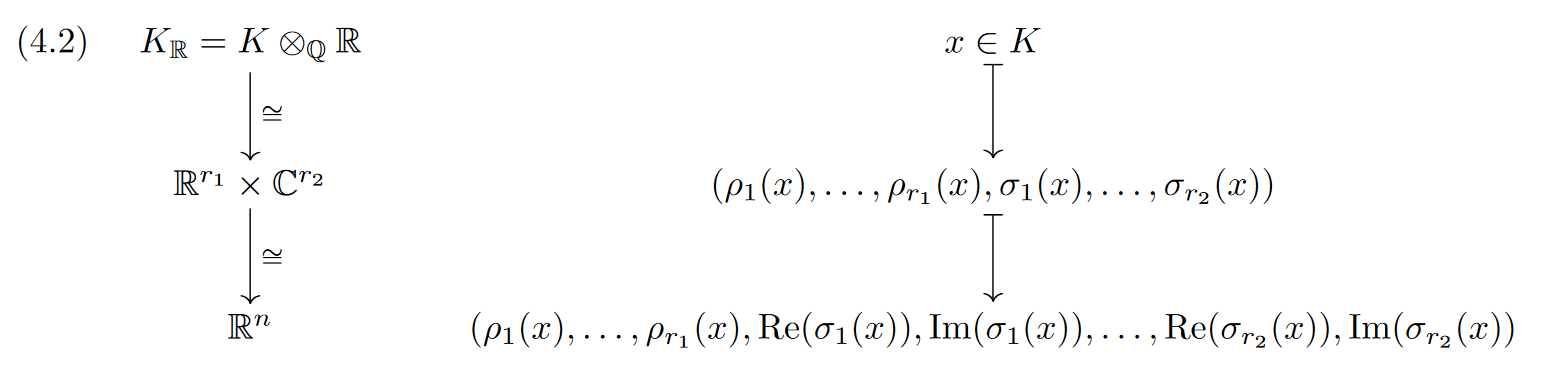 
Then, we can view $\mathcal O_K$ and any fractional ideal a as lattices in the Euclidean space $K_{\mathbb R} \cong {\mathbb R}^n$.
为了能更加精确的刻画这种把代数整数分开的感觉，我们需要严格定义何为格点
Def. A sub group of $\Gamma \subset \mathbb R^n$ is
- alattice if it is free of rank $n$ and containing a basis of $\mathbb R^n$;
- discrete if any $\gamma \in \Gamma$ has an open neighborhood $U \subset \mathbb R^n$ such that $U \cap \Gamma = {\gamma}$;
- cocompact if there exist a compact subset $\Omega \subset \mathbb R^n$ whose translates by $\Gamma$ over $\mathbb R^n$.
Next section
这一节中我们分类了