orientation-preserving homeomorphism on $S^1$

In this note, we will talk about the dynamic system of homeomorphism on $S^1$.

$\alpha$-limit and $\omega$-limit of $S^1$

$\rho: S^1 \to S^1$ orient-preserve homeomophism. We can define $\omega$-limit and $\alpha$-limit sets of $x \in S^1$: \(\omega(x) :=\{y \in S^1: \exists m_i \to +\infty \text{ s.t. } \rho^{m_i}(x) \to y \text{ as }i\to+\infty\}\) \(\alpha(x) :=\{y \in S^1: \exists m_i \to -\infty \text{ s.t. } \rho^{m_i}(x) \to y \text{ as }i\to+\infty\}\)

Example. $\rho = \mathrm R_\alpha, \alpha \in \mathbb R - \mathbb Q \Rightarrow \omega(x)=S^1,\alpha(x)=s^1\forall x \in S^1$

Prop. If $\rho(f) \in \mathbb R - \mathbb Q$, then $\omega(x)=\omega(y)\forall x \not = y \in S^1$

To prove this proposition, we need a lemma below.

Lemma. Assume $\rho(f) \in \mathbb R - \mathbb Q$. Let $x,z \in S^1, m > n \in \mathbb N$, and let $I = [\rho^n(x), \rho^m(x)]\subset S^1$. Then, $\exists k \in \mathbb N^*$ s.t. $\rho^k(z)\in I$.

proof of lemma. The intervals $\rho^{-k(m-n)}(I)$ and $\rho^{-(k-1)(m-n)}(I)$ have a common boundary. Then, we have two case: case1: If ${\rho^{-k(m-n)}(I)}$ not cover $S^1$ by finite union. $\sum_{k=1}^\infty l(\rho^{-k(m-n)}(I)) \le l(S^1)$ converge That is, the boundary point of $\rho^{-k(m-n)}(I)$ converge to one point $y \in S^1$, implies $\rho^{-k(m-n)}(I)$ converge to the point $y \in S^1$. Since $\rho^{-(m-n)}(y) = y$, implies $y$ is a periodic point of $\rho$, an contraction. case2: $\sum_{k=1}^\infty l(\rho^{-k(m-n)}(I))$ not converge Then, $\sum_{k=1}^N l(\rho^{-k(m-n)}(I)) \to \infty$, $S^1$ will be covered finite of ${\rho^{-k(m-n)}(I)}$. That is, there exist $k_0 \in \mathbb N$ s.t. $z_0 \in \rho^{-k(m-n)}(I)$. Hence, $\rho^{k(m-n)}(z) \in I$.

proof of thm. $\rho (f) \in \mathbb R - \mathbb Q$, $x \not = y \in S^1$ we want to show that $\omega (x) = \omega(y)$ First, we choose $x_0 \in \omega(x)$, then $\exists m_i \to +\infty$ s.t. $\rho^{m_i}(x) \to x_0$. By the lemma, $\exists k_i \in \mathbb N$ s.t. $\rho^{k_i}(y) \in [\rho^{n_i}(x), \rho^{n_i + 1}(x)]$. Without losing generality, we can choose $k_{i+1} > k_i, \forall i$ so that $k_i \to +\infty$ as $i\to +\infty$. Since $\rho^{n_i}(x) \to x_0$, we obtain $\rho^{k_i}(y) \to x_0$. Then, $x_0 \in \omega(y)$ implies $\omega(x) \subset \omega(y)$. By summetry, we also have $\omega(y) \subset \omega(x)$. Hence, $\omega(x) = \omega(y)$.

periodic point of $\rho(f) \in \mathbb Q$

Thm. $\rho(f) = \frac{p}{q} \in \mathbb Q$, then for any point $x \in S^1$ (i) $x$ is $q$-periodic, or (ii) $\exists$ $q$-periodic point $x_0 \in S^1$ s.t. $| f^m(x)-f^m(x_0)| \to 0$ as $m \to +\infty$.

proof. Let $F$ is a lift of $f$ with $\rho(F) = \frac p q$, then we have $\rho(F^q - p) = 0$. Define $G = F^q - p$, we claim that $G$ has a fix point.

Topological conjugacy

Let $f,g: S^1 \to S^1$ be orientation-preserveing homeomorphism, we say $f$ and $g$ are conjugate iff $\exists$ orientation-preserving homeomorphism $h: S^1 \to S^1$ s.t. $h \circ f = g \circ h$.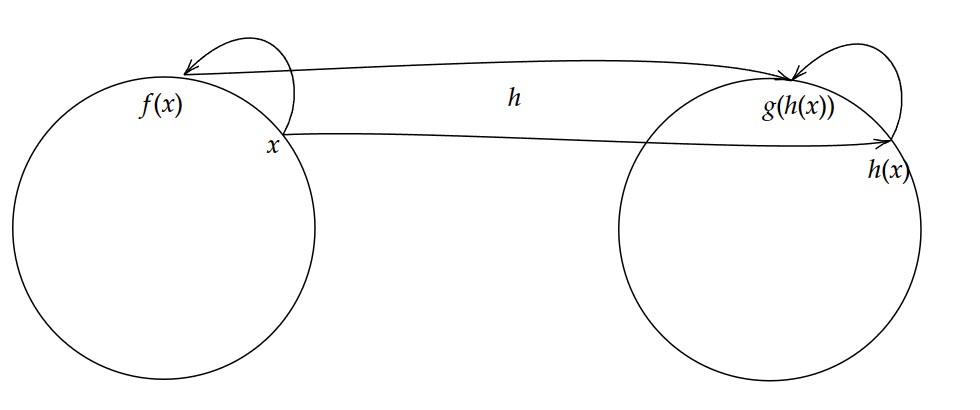

Prop. If $f$ and $g$ are conjugate, then $\rho(f) = \rho(g)$.

Prop. $\rho(f) = \alpha \in \mathbb R - \mathbb Q$, $F:\mathbb R \to \mathbb R$ lift of $f$. Set $x_0 \in \mathbb R$, let $\omega(x_0) = {F^i(x_0) + j: i,j \in \mathbb R}$ extended orbit of $x_0$. Define $\overline{H} : \omega(x_0) \to \mathbb R; F^i(x_0) + j \mapsto i \alpha + j$ Then, $\overline H$ is actually increasing.

Prop. $\rho(f) = \alpha \in \mathbb R - \mathbb Q$, Then $\exists$ a semi-conjugacy $h:S^1 \to S^1$ between $f$ and $R_\alpha$. i.e. $h$ is a surjective and continuous map of degree $1$ s.t. $h \circ f = R_\alpha \circ h$.

有了半共轭的这个放松了很多的条件，但是出乎意料的是，这个结构并不够强

Def. A homeomorphism $f:S^1 \to S^1$ is called a diffeomorphism iff $f$ and $f^{-1}$ are differentiable (i.e. $F$ and $F^{-1}$ are differentiable) we say that $f: S^1 \to S^1$ is $C^1$ iff $f$ is differentiable and $f’$ is continuous.

Thm. (Denjoy example) given $\alpha \in \mathbb R \backslash \mathbb Q$, there exist a $C^1$-orientation-preserving diffeomorphism $f:S^1 \to S^1$ with $\rho(f)=\alpha(\text{mod } 1)$ such that $f$ has no dense hajectory.

这个定理，直接构造即可，这边便不过多赘述，可以参考