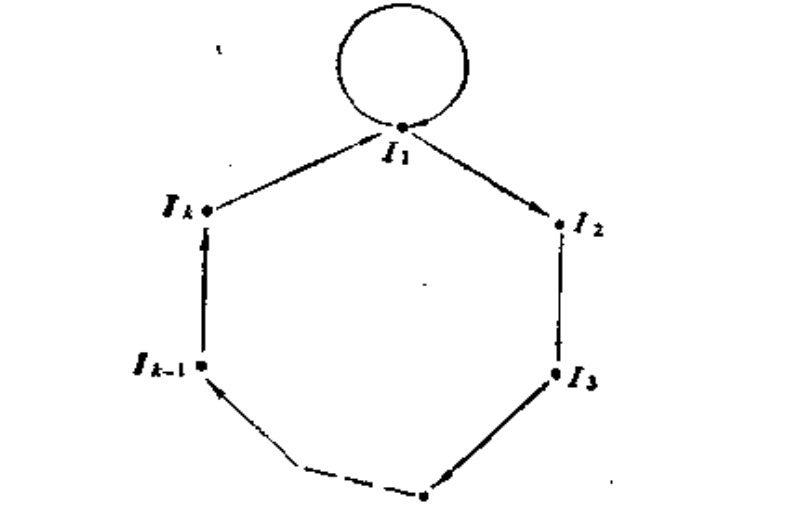
动力系统 Sarkovski定理

title: ‘Sarkovski定理-三即混沌’ date: 2023-10-11 tags:

• learning notes

• dynamic system

Theorem Let $f:\mathbb R \to \mathbb R$ be continuous. Suppose $f$ has a periodic point of period $3$ Then $f$ has periodic point of all other periods.

三即混沌

Lemma $J = [a,b]$ compact interval If $f(J) \supset J$, then $f$ has a fixed point in $J$.

sketch of proof. Using Zero point theorem in math analysis.

Lemma $J=[a,b]$, $I = [a,b]$ If $f(J) \subset I$, then $\exists J’ \subset J$ subinterval s.t. $f(J’)=J$.

proof. Since $f(J) \subset I$, there exist $\alpha, \beta \in J$ such that $f(\alpha) = a, f(\beta) = b$. without lose of generation, we can assume $\alpha < \beta$. \(c = \sup\{c' \in J : c' < \beta, f(c')=a\}\) \(d = \inf\{d' \in J : c < d', f(d')=b\}\) $J’ = [c,d]$ is what we need.

proof of the theorem. we can assume $a<b<c \in \mathbb R$, such that $b = f(a), c = f(b), a = f(c)$.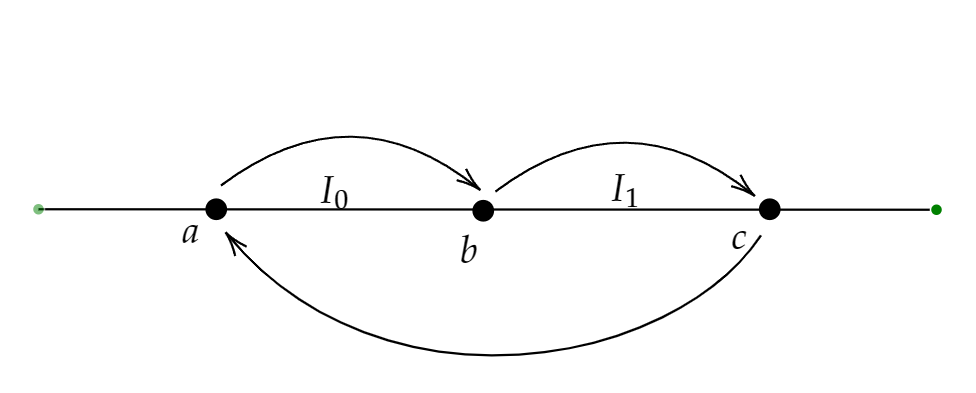

Let $n \ge 4$. Set $A_0 = I_1$,. Since $f(A_0) \supset I_1, \exists A_1 \supset A_0 s.t.f(A_1) = A_0$ Since $f(A_1) \supset A_0, \exists A_2 \supset A_1 s.t.f(A_2) = A_1$. \(\vdots\) Since $f(A_{n-3}) \supset A_{n-3}, \exists A_{n-2} \supset A_{n-3} s.t.f(A_{n-2}) = A_{n-3}$. Since $f(I_1) \supset I_0$ and $f^{n-2}(A_{n-2}) = I_1$, then there exist $A_{n-1} \subset A_{n-2}$ s.t. $f^{n-1}(A_{n-1}) = I_0$.

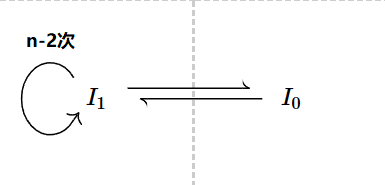
Then we have $f^n (A_{n-1}) = f(I_0) \supset I_1 \supset A_{n-1}$ $\Rightarrow f^n$ has a fixed point $x_n$ in $A_{n-1}$ $f^n(x_n) = x_n$ $f(x_n) \in I_1$ $\vdots$ $f^{n-2}(x_n) \in I_1$ $f^n(x_n) \in I_0$

Thus, $x_n$ is what we need.

Sarkovski theorem

actually, we can defind sarkovski order as below: \(3 > 5 > 7 > 9 > \cdots > 2\cdot3 > 2\cdot5>\cdots\) \(> 2^2\cdot3> 2^2\cdot5 > \cdots > 2^m\cdot3> 2^m\cdot5 > \cdots\) \(> 2^m > \cdots > 2^2 > 2 > 1\)

Then, we have a more generate theorem

Thm. $f : \mathbb R \to \mathbb R$ continuous. Suppose $f$ has a periodic point of prime period $n$. If $n \ge k$, then $f$ has point with periodic $k$.