热力学第二定律(熵增定律)
Published:
热力学第二定律 笔记
本博客为读者学习笔记,如有错误,恳请指出。
本笔记图片源自《Principles of Physics》,其余部分禁止转载
热力学第二定律(熵增定理)
If a process occurs in a closed system, the entropy of the system increases for irreversible processes and remains constant for reversible processes; it never decreases.
在一个封闭系统中,不可能把热量从低温物体传递到高温物体而不产生其他影响
————Rudolf Clausius (1822-1888)
The energy of the universe id constant.
The entropy of the universe tends to a maximum.
有意思的是,此前所有物理定律都没有指出该过程不可逆。该定理打破了物理理论在时间上的对称性。可以说,该定理引出了时间的单向性
熵 S
我们定义 \(S = \frac{Q}{T}\) 称之为熵
气体过程 熵的变化
我们记$i$为初始状态(initial state), $f$为最终状态(final state). \(\Delta S = S_f - S_i = \int_{i}^{f} \mathrm{d} S = \int_{i}^{f} \frac{\mathrm{d} Q}{T} = \int_{i}^{f} \frac{\mathrm{d} E_{int} + \mathrm{d} W}{T}\)
等压变化(Isobaric process)
\[\Delta S = n R \mathrm{ln} \frac{V_f}{V_i} + n C_V \mathrm{ln} \frac{T_f}{T_i} = n C_p \mathrm{ln} \frac{T_f}{T_i}\]等温变化(Isothermal process)
\[\Delta S = n R \mathrm{ln} \frac{V_f}{V_i} = \frac{Q}{T}\]绝热变化(Adiabatic process)
\[dQ \equiv 0 , \Delta S = 0\]等容变化(Isochoric process)
\[\Delta S = n C_V \mathrm{ln} \frac{T_f}{T_i} = n C_V \mathrm{ln} \frac{P_f}{P_i}\]自由扩散(irreversible process)
\[T_i = T_f ; \Delta S = n R \mathrm{ln} \frac{V_f}{V_i} = n R \mathrm{ln} \frac{P_i}{P_f}\]熵的变化
粒子数目越多,熵就越高
\[S = k \cdot \mathrm{ln}W\]微观诠释(非严谨)
若是取n个粒子,两个相同的盒子,盒子联通,假设对一个粒子在任意盒子中的概率相同。记在同一盒子中的数目为N。计算 \(\mathrm{P}(N=m) = \frac{n!}{(n-m)!m!}\) 当n增加时,$\mathrm{P}(N=N/2)$将远远大于$\mathrm{P}(N=0)$即高熵态概率更高。
记粒子总数$N$,粒子两种状态$n_1, n_2$ \(W = \frac{N!}{n_1! n_2!}\) 当$n$足够大时, \(\mathrm{ln} N ! \approx N(\mathrm{ln} N) - N\)
热力学的妖精
物理学四大神兽之一 ——麦克斯韦妖
一个绝热容器被分成相等的两格,中间是由“妖”控制的一扇小“门”,容器中的空气分子作无规则热运动时会向门上撞击,“门”可以选择性的将速度较快的分子放入一格,而较慢的分子放入另一格,这样,其中的一格就会比另外一格温度高。
用这个理论,麦克斯韦创造出了一个看似违反热力学第二定律的情况。
因为麦克斯韦妖与气体之间只有信息交换,没有能量交换,当时的物理学一直没有办法解释清楚。
信息熵
香农提出了信息熵的概念
信息的基本作用就是消除人们对事物的不确定性。那么如果我们已知出现事件的概率,那么我们需要用多少熵去记录它呢。于是,香农把信息冗余度与热力学的熵联系到了一起。 \(H(U) = E[- \mathrm{log} p_i] = - \sum_{i=1}^{n}p_i \mathrm{log} p_i\) 至此,物理学家才成功解释麦克斯韦妖。
热机
热机的效率
\[\varepsilon = \frac{我们得到的能量}{我们输入的能量} = \frac{\left | W \right |}{\left | Q_H \right |} = 1 - \frac{|Q_L|}{|Q_H|}\]显然,我们有$0 \le \varepsilon < 1$.
卡诺(Carnot)循环
如下图所示
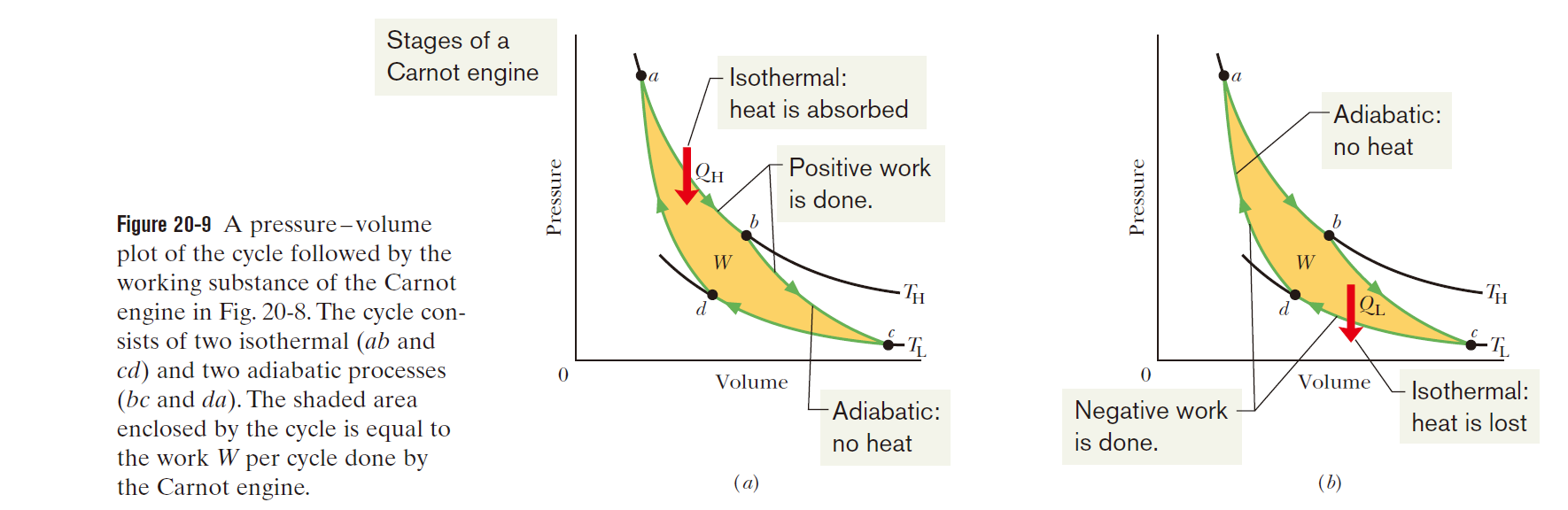
即,等温过程与绝热过程交替进行,高温膨胀,绝热膨胀,低温收缩,绝热收缩。
符合卡诺循环的热机的效率$\varepsilon_C$可以用以下公式计算 \(\varepsilon_C = 1 - \frac{\left | Q_L \right | }{\left | Q_H \right | } = 1 - \frac{T_L}{T_H}\)
斯特林(stirling)循环
如下图所示
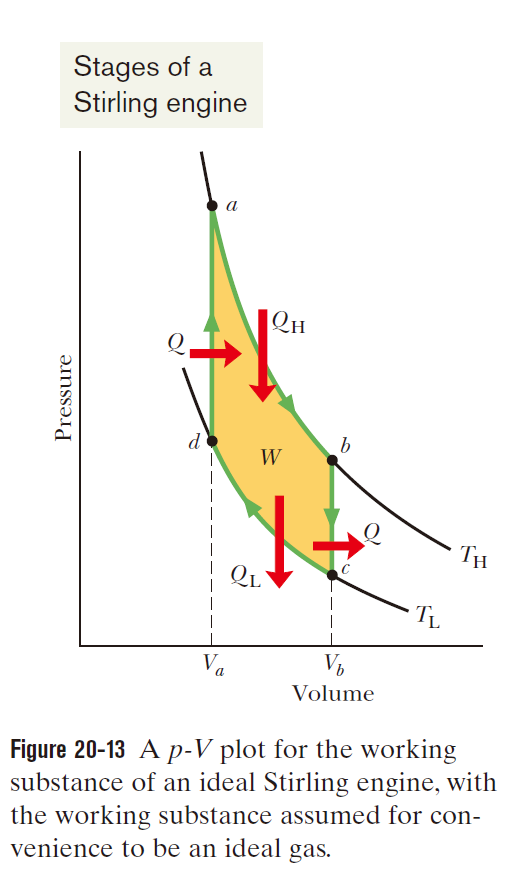
即等温变化与等容变化交替进行。
Otto 热机
较为常用的热机,指等容变化与绝热变化交替进行。
热机的逆运算(雾)——制冷
通过外加能量使得热机做功进程逆转,从而达到制冷的效果。
冰箱的表现系数(The coefficient of performance) \(K = \frac{\text{what we want}}{\text{what we pay for}} = \frac{|Q_L|}{|W|} = \frac{|Q_L|}{|Q_H| - |Q_L|}\)
卡诺冰箱(Carnot refrigerator )
即卡诺循环逆向进行的结果
特别的, \(K_C = \frac{T_L}{T_H - T_L}\)
