前言

1 傅里叶级数

\(f \sim \sum a_n e^{inx}\) \(a_n = \frac{1}{2\pi}\int_{-\pi}^{\pi} f(x)e^{-inx}dx\) 由此我们可以得到Parseval恒等式： \(\sum_{n=-\infty}^{+\infty} |a_n|^2 = \frac{1}{2\pi}\int_{-\pi}^\pi |f(x)|^2 dx\) 在常庚哲,史济怀的《数学分析》中也有相关论述： 但是这样得到的度量，并非完备

前置知识储备

集合与度量

点 point

A point $x \in \mathbb R^n$ consists of a $d$-tuple of real numbers \(x=(x_1,x_2,\dots,x_d), x_i \in \mathbb R,\text{ for }i=1,\dots,d\)

范数 norm

The norm of x is denoted by $|x|$ and is defined to be the standard Euclidean norm given by \(|x| = (x_1^2+\cdots+x_d^2)^{1/2}\)

补集 complement

The complement of a set $E$ in $\mathbb R^d$ is denoted by $E^c$ and defined by \(E^c = \{x \in \mathbb R^d : x \not \in E\}\)

距离 distance

The distance between two points $x$ and $y$ is then simply $|x-y|$. The distance beteween two sets $E$ and $F$ is defined by \(d(E,F) = \inf_{x\in E,y \in F} |x-y|\)

点与点之间的位置关系——开、闭、紧致集

The open ball in $\mathbb R ^ d$ centered at $x$ and of radius $r$ is defined by \(B_r(x) = \{y \in \mathbb R^d : |y-x| < r\}\) A subset $E \subset \mathbb R^d$ is open if for every $x \in E$ there exists $r > 0$ with $B_r(x) \subset E$. A subset $E \subset \mathbb R^d$ is closed if its complement is open. A subset $E \subset \mathbb R^d$ is bounded if it is contained in some ball of finite radius.

A subset $E \subset \mathbb R^d$ is compact if it is closed and bounded.warning: 这只在欧氏空间中成立 A subset $E \subset \mathbb R^d$ is compact if there is a finite subcovering for any open covering.

A point $x \in\mathbb R^d$ is a limit point of the set $E$ if for every $r> 0$, the ball $B_r(x)$ contains points of $E$. An isolated point of E is a point $x \in E$ such that there exists an $r > 0$ where $B_r(x) \cap E$ is equal to ${x}$. A point $x \in E$ is an interior point of $E$ if there exists $r > 0$ such that $B_r(x) \subset E$.

The set of all interior points of $E$ is called the interior of E. the closure $E$ of the $E$ consists of the union of $E$ and all its limit points. The boundary of a set $E$, denoted by $\partial E$, is the set of points which are in the closure of $E$ but not in the interior of $E$. 内部是被$E$包含的最大开集，闭包是包含$E$的最小闭集。

a closed set $E$ is perfect if $E$ does not have any isolated points.

最直接的体积计算——长方形

A (closed) rectangle $R$ in $\mathbb R^d$ is given by the product of $d$ one-dimensional closed and bounded intervals \(R = [a_1, b_1] \times [a_2, b_2] \times \cdots \times [a_d, b_d]\) The volume of the rectangle $R$ is defined as \(|R| = (b_1 - a_1)\cdots(b_d-a_d)\) a cube is a rectangle for which $b_1 - a_1 = \cdots = b_d-a_d$, whose volume is $(b_1-a_1)^d$

A union of rectangles is said to be almost disjoint if the interiors of the rectangles are disjoint.

Lemma 1.1

If a rectangle is the almost disjoint union of finitely many other rectangles, say $R = \bigcup_{k=1}^N R_k$, then

proof. 如下图，进行有限次划分，进而变成我们更加容易处理的形式。 \(|R| = \sum_{j=1}^M |\overline{R_j}| = \sum_{k=1}^N\sum_{j \in J_k}|\overline{R_j}| = \sum_{k=1}^{N}|R_k|\)

Lemma 1.2

If $R, R_1, \dots , R_N$ are rectangles, and $R \subset \bigcup^N_{k=1} R_k$, then $

R

\le \sum^N_{k=1}

R_k

$.

proof. 和Lemma 1.1相似的方法，将矩形分割，将面积累加。而重叠的部分则是不等的缘由

Lemma 1.3

Every open subset $\mathcal{O}$ of $\mathbb R$ can be writen uniquely as a countable union of disjoint open intervals.

proof. Consider \(a_x = \inf\{a<x:(a,x) \subset \mathcal{O}\}, b_x = \inf\{b>x:(x,b) \subset \mathcal{O}\}\) Since $I_x = (a_x,b_x)$ is a subset of $\mathcal O$, then we have \(\mathcal O = \bigcup_{x\in\mathcal O} I_x\) If $I_x \cap I_y \not = \emptyset$, then $I_x \cup I_y$ is also a interval. Then we have $I_x \cup I_y \subset I_x$ and $I_x \cup I_y \subset I_x$ by definition. This only happen when $I_x = I_y$. Since every open interval contain a rational number, we can choose disjoint rational number for every element in ${I_x}{x \in \mathcal O}$, since they are disjoint. Therefore, ${I_x}{x \in \mathcal O}$ is countable.

Lemma 1.4

Every open subset $\mathcal O$ of $\mathbb R^d, d \ge 1$, can be written as a countable union of almost disjoint closed cubes.

proof. 先用长度为1的正方形划分$\mathbb R^d$，标记被$\mathcal O$包含的正方形为$Q_{1,1},Q_{1,2},Q_{1,3},\dots$ 再使用更细的划分去填补剩下的空间，每一次都将边长变成原来的1/2. 因为每一层都最多使用可数个正方形，而总共有可数层，于是总计使用的正方形数量不会超过可数个。 而对于开集$\mathcal O$中的每一个点$x$, 都存在一个以$x$为中心半径为$\delta$的球被包含在开集$\mathcal O$内, 因此必然存在边长大于$\delta / 2$的划分使得该点被正方形覆盖。 因此，the open set $\mathcal O$ can be written as a countable union of almost disjoint closed cubes

康托尔集 Cantor set

The total length of Cantor set is 0. （但这个说法对于现在的我们来说很符合直觉但不严谨，你如何去测量一个有无穷断点的物体的长度呢？

外测度 exterior measure

由上面的定理，我们知道，一个相对规整的集合（比如开集）可以表示为可数个正方形的无交并，这预示着我们去利用已知的正方形的体积去测量任意集合的体积 当我们用多个正方形从外侧去逼近一个图形的时候，也许就可以得到一些与面积相关的信息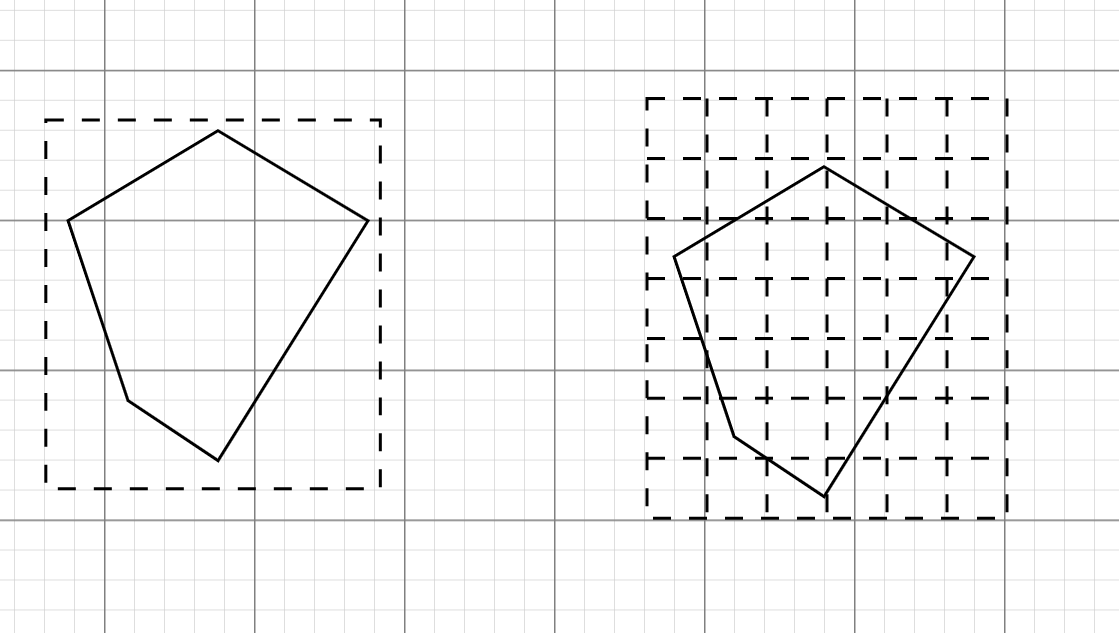

定义外测度

The precise definition is as follows: if $E$ is any subset of $\mathbb R^d$, the exterior measure of $E$ is \(m_*(E) = inf\{\sum_{j=1}^\infty |Q_j|\}\)

值得注意

1 这里使用有限和是有可能得不到我们想要的面积的

比如说$[0,1]$中所有有理数构成的集合$E$，在有限和定义的测度下测度为1，但是数学分析告诉我们这应该是一个零测集。

2 事实上可以将正方形替换成长方形，这个定义依然生效

可以试试将长方形用可数个正方形表达出来

试试手

Example 1

The exterior measure of a point is zero.

Example 2

The exterior measure of a closed cube is equal to its volume.

Example 3

If $Q$ is an open cube, the result $m_∗(Q) =

Q

$ still holds.

Example 4

The exterior measure of $\mathbb R^d$ is infinite.

Example 5

The Cantor set $\mathcal C$ has exterior measure $0$.

外测度的性质

观察所得

观察所见，加上少许证明，即为基本的性质。

Obs1

$A \subset B \Rightarrow m_(A) \le m_(B)$

因为任何一个$B$的覆盖也是$A$的一个覆盖。

Obs2

若$J$可数，则$m_(\bigcup_{j \in J} A_j) \le \sum_{j \in J} m_(A_j)$

By definition, we get a covering $E_j \subset \bigcup_{k=1}^\infty Q_{k,j}$ such that \(\sum_{k=1}^{\infty} |Q_{k,j}| < m_*(E_j) + \frac{\epsilon}{2^j}\) Then, we have \(m_*(E) \le \sum_{j=1}^\infty \sum_{k=1}^\infty|Q_{k,j}| \le \sum_{j=1}^\infty \left(m_*(E) + \frac{\epsilon}{2^j}\right) \le \sum_{j=1}^\infty m_*(E) + \epsilon\)

Obs3

If $E \subset \mathbb R^d$, then $m_∗(E) = \inf m_∗(\mathcal O)$, where the infimum is taken over all open sets $\mathcal O$ containing $E$.

Obs4

If $E = E_1 \cup E_2$, and $d(E_1, E_2) > 0$, then $m_∗(E) = m_∗(E_1) + m_∗(E_2)$.

By Obs2, we have $m_(E) \le m_(E_1) + m_*(E_2)$.

Obs5

If a set $E$ is the countable union of almost disjoint cubes $E = \bigcup_ {j=1}^\infty Q_j$, then

测度公理化

1. （Borel性质）$\mathbb R^n$中每一个开集都是可测集，每一个闭集都是可测集。
2. （补性质）如果$\Omega$是可测的，那么$\mathbb R^n / \Omega$也是可测的
3. （Boole代数性质）如果$(\Omega_j){j \in J}$是可测集的有限族，那么$\bigcup{j \in J} \Omega_j$和$\bigcap_{j \in J} \Omega_j$都是可测集
4. （$\sigma$代数性质）如果$(\Omega_j){j \in J}$是可测集的可数族，那么$\bigcup{j \in J} \Omega_j$和$\bigcap_{j \in J} \Omega_j$都是可测集
5. $m(\emptyset) = 0$
6. $0\le m(\Omega) \le \infty$
7. $A \subset B \Rightarrow m(A) \le m(B)$
8. 若$J$可数，则$m(\bigcup_{j \in J} A_j) \le \sum_{j \in J} m(A_j)$
9. 若$(A_j){j\in J}$ 是互不相交的可数族，则$m(\bigcup{j \in J} A_j) =\le= \sum_{j \in J} m(A_j)$
10. （正规化性质）$m([0,1]^n)=1$
11. 若$\Omega$是可测集而$x \in \mathbb R^n$，那么$x+\Omega := {x+y:y\in\Omega}$是可测的，而且$m(x+\Omega) = m(\Omega)$.