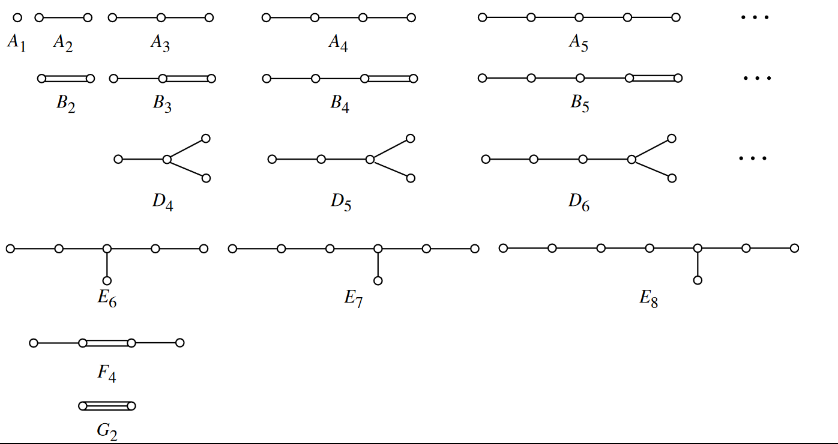
Dynkin_graph

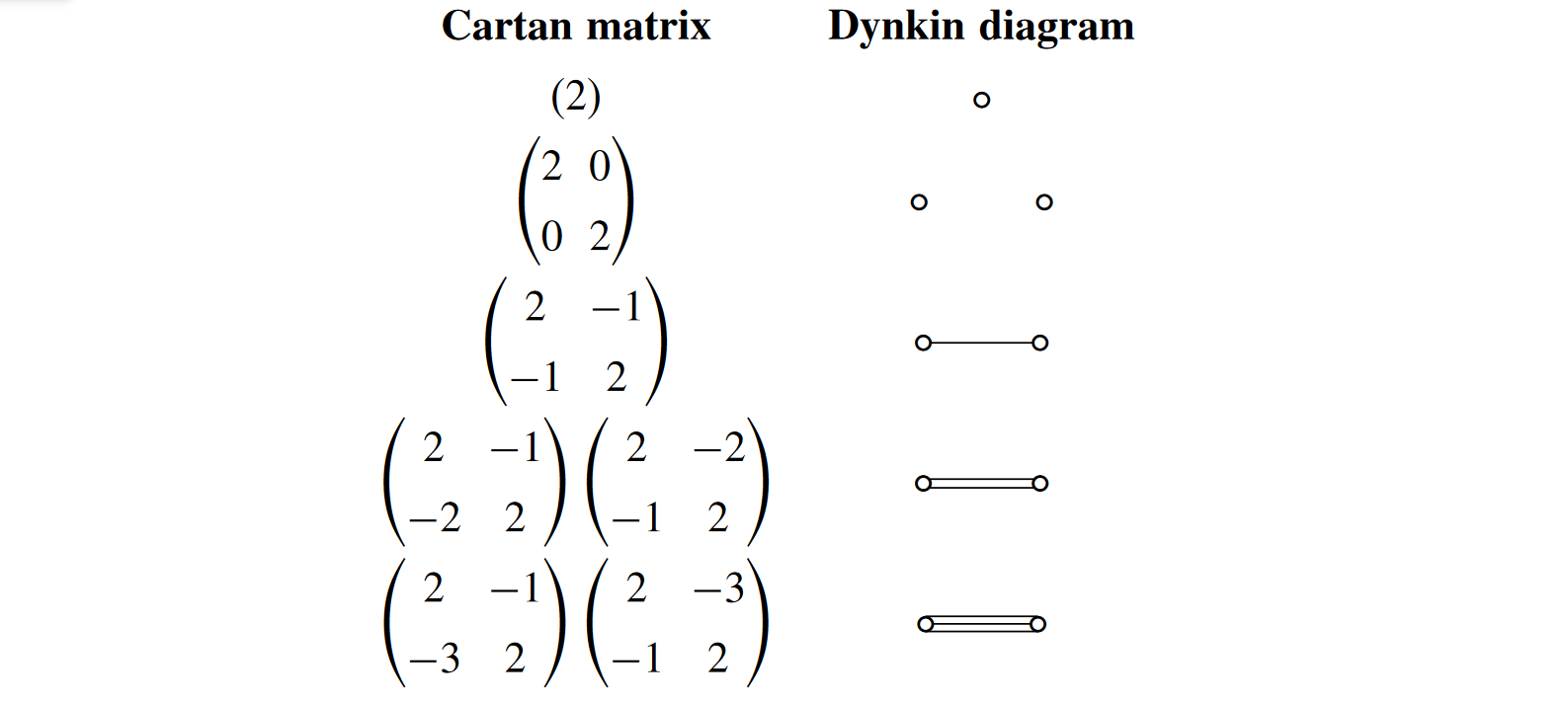
Def. Cartan matrix \(A_{ij} = 2 \frac{<\alpha _i, \alpha_j>}{<\alpha _i, \alpha_i>},i,j \in 1, \dots, l\)

Prop. The Cartan matrix $A$ has the following properties.

Def. Dynkin diagram The Dynkin diagram is determind by the Cartan matrix. It is a graph with wertices labelled $1, \dots, l$. If $i \not = j$ the vertices are joined by $n_{ij}$ edges, where \(n_{ij} = A_{ij}A_{ji}\)

The quadratic form \(Q(x_1, \dots, x_l) = 2 \sum_{i = 1}^l x_i ^2 - \sum_{i,j=1,i\not = 1}^l \sqrt{n_{ij}} x_i x_j\)

Prop. $Q(x_1, \dots, x_l)$ is positive difinite.

Lemma. let $(V, \Phi)$ be a root system. If $V = V_1 \oplus V_2$ and $\Phi \subset V_1 \cup V_2$, then 1)$V_1 \perp V_2$ 2)$(V_1, \Phi \cap V_1)$ and $(V_2, \Phi \cap V_2)$ are reduced root system.

(A) The graph is connected. (B) Any pair of distinct vertices are joined by $0,1,2$ or $3$ edges. (C) The corresponding quadratic form $Q(x_1, \dots, x_l)$ is positive definite.