黎曼几何：流形和流形上的故事

补充一些基础的微分流形知识

Regular surface

regular surface on $\mathbb R^n$

在 $\mathbb R^n$ 有一些最直接的曲面，

Def. regular surface A subset $M \subset \mathbb R ^n$ is called a regular surface if for each point $p \in M$, there exists a neighborhood $V$ of $p$ in $\mathbb R^n$ and a map $x:U\to R^n$ of an open set $U subset R^2$ onto $V \cap U$ such that 1. $\mathbf x$ is differentiable, 2. $\mathbf x:U \to V \cap M$ is a homeomorphism, and 3. $(d \mathbf x)_q : \mathbb R^k \to \mathbb R^n$ is injective for all $q \in U$.

Any open subset of a regular surface is also a regular surface.

Thm. for any two parametrizations $\mathbf x: U \subset \mathbb R^k \to M^k$, $\mathbf y: V \subset \mathbb R^k \to M^k$, with $\mathbf x (U) \cap \mathbf y(V) = W \not = \emptyset$. Then, $h =\mathbf x ^{-1} \circ \mathbf y: \mathbf y ^{-1}(W) \to \mathbf x ^{-1}(W)$ is a diffeomorphism.

proof. Firstly, we observe that $h$ is a homeomophism, since $h$ is the composition of two homeomorphism. Let $r \in \mathbf y^{-1}(W)$ and $q = h(r)$. Denote $(u_1, \dots u_k) \in U$ and $(v_1, \dots, v_n) \in V$, then we can write $\mathbf x(u_1,\dots,u_k) = (v_1(u1,\dots,u_k), \dots, v_n(u1,\dots,u_k))$. By condition (3), we can suppose that \(\frac{\partial(v_1,\dots,v_k)}{\partial (u_1,\dots, u_k)}(q) \not = 0\) (大不了换一下$U$各个维度的次序) Extend $\mathbf x$ to a mapping $F: U\times \mathbb R^{n-k} \to \mathbb R^n$ given by \(\begin{eqnarray} &&F(u_1,\dots,u_k,t_{k+1},\dots,t_n)\\ & = & (v_1(u_1,\dots,u_k),\dots,v_k(u_1,\dots,u_k),\\ &&v_{k+1}(u_1,\dots,u_k)+t_{k+1},\dots,v_{n}(u_1,\dots,u_k)+t_{n}) \end{eqnarray}\) Then, $F$ is differentiable and $F|_{U\times(0,\dots,0)} = \mathbf x$.

$$ \det (dF_q) = \det\begin{pmatrix} \frac{\partial v_1}{\partial u_1} & \cdots & \frac{\partial v_1}{\partial u_k} & & &
\vdots & \ddots & & &&
\frac{\partial v_k}{\partial u_1} & & \frac{\partial v_k}{\partial u_k} & & &\

• & * & * & 1 & &\
• & * & * & & \ddots &\
• & * & * & & &1 \end{pmatrix} = \frac{\partial(v_1,\dots,v_k)}{\partial (u_1,\dots, u_k)}(q) \not = 0 $$ We are then able to apply the inverse function theorem, which guarantees the existence of a neighborhood $Q$ of $\mathbf x(q)$ where $F^{-1}$ exist and differentiable. Since $\mathbf y$ is continuous, then exist $R$ s.t. $\mathbf y(R) \subset Q$. Then $h|_R = F^{-1} \circ \mathbf y|_R$ is differentiable at $r$. Hence, $h$ is differentiable in $\mathbf y ^{-1} (W)$. A similar arguement would show that $h^{-1}$ is differentiable as well, which finish the prove.

Now, we will show another way to construct a regular surface.

Inverse image of regular value

In this section, we let $F:U \subset \mathbb R^n \to \mathbb R^m$ be a differentiable mapping of an open set $U$ of $\mathbb R^n$.

Def. critical point and critical value a point $p \in U$ and $dF_p:\mathbb R^n \to \mathbb R^m$ is not surjective, $p$ called critical point. the image $F(p)$ callled critical value.

Def. regular value a point $a \in \mathbb R^m that is not a critical value.

Any $a \not \in F(U)$ is a regular value. If there exist a regular value of $F$ in $\mathbb R^m$, then $n \ge m$.

Thm. Let $a \in F(U)$ be a regular value of $F$, then $F^{-1}(a) \subset \mathbb R^n$ is a regular suface of dimension $k = n-m$.

proof. Let $p \in F^{-1}(a)$. Denote $q = (y_1,\dots,y_m,x_1,\dots,x_k)$ is a arbitary point in $\mathbb R^{n = m+k}$, and $F(q) = (f_1(q),\dots,f_m(q))$ its image by mapping $F$. We want to build up a parametrization from the mapping $F$, because $F$ produce all the imformation of the inverse image $F^{-1}(a)$. Since $a$ is a regular value, $dF_p$ is surjective. Therefore, we can suppose \(\frac{\partial(f_1,\dots,f_m)}{\partial(y_1, \dots,y_m)} (q)\not =0\) To use the inverse function theorem, we extend $F$ to a mapping $\varphi: U \subset \mathbb R^n \to \mathbb R^{n = m+k}$ by \(\varphi(y_1,\dots,y_m,x_1,\dots,x_k) = (f_1(q), \dots,f_m(q),x_1,\dots,x_k)\) Then\(\det(d\varphi)_p = \frac{\partial(f_1,\dots,f_m)}{\partial(y_1, \dots,y_m)} (q)\not =0\) By the inverse function theorem, $\varphi$ is a diffeomorphism of a neighborhood $Q$ of $p$ onto a neightborhood $W$ of $\varphi(p)$. Choose a compact cube $K^{m+k} \subset W \subset \mathbb R^{n=m+k}$ which have the center $\varphi(p)$. Define $\mathbf x = \varphi^{-1}|_{{a} \times K^{k} }$ on $K^{k}$.(这里记号有点混乱，可能需要一张图) Then, $\mathbf x$ is a mapping satisfied the conditions of regular suface. Since $p$ is arbitrary, then $F^{-1}(a)$ is a regular surface in $\mathbb R^n$.

Orientable manifold

orientable

Def. Let $M$ be a differentiable manifold. We say that $M$ is orientable if $M$ adimits a differentiable structure ${(U_\alpha , \mathbf{x}\alpha)}$ such that: (i) for every pair $\alpha,\beta$, with $\mathbf x\alpha(U_\alpha) \cap \mathbf x_\beta(U_\beta) = W \not = \emptyset$, $\det (\mathbf x_\alpha^{-1}\circ \mathbf x _\beta)$ is positive.

In the opposite case, we call $M$ is non-orientable. If $M$ orientable, a choice of a differentiable structure satisfying (i) is called an orientation of $M$. $M$ is said oriented. Two differentiable structures that determine the same orentation if their union again satisfied (i).

Let $M_1$ and $M_2$ is two orientable manifold, $\varphi: M_1 \to M_2$ is a diffeomorphism. Then, $M_1$ orientable $\Leftrightarrow$ $M_2$ orientable. If, additionally, $M_1$ and $M_2$ is oriented and connected, $\varphi$ induce a orientation on $M_2$ If it coincide the initial orientation of $M_2$, then we said $\varphi$ preserve the orientation. If not, we said $\varphi$ reserve the orientation.

Thm. If $M$ can be covered by two coordinate neighborhoods $V_1$ and $V_2$ in such a way that the intersection $V_1\cap V_2$ is connected, then $M$ is orientable.

Proof. Since $\det (\mathbf x_1 ^{-1} \circ \mathbf x_2)$ is continuous, then it will not change the sign on $V_1 \cap V_2$. We can change the sign of $\mathbf x_1$ if necessary, then $\det (\mathbf x_1 ^{-1} \circ \mathbf x_2)$ will always positive.

Example. \(S^n=\left\{ (x_1,\dots,x_{n+1}) \in \mathbb R^{n+1}; \sum_{i=1}^{n+1} x_i^2 = 1 \right\} \subset \mathbb R^{n+1}\) is orientable.

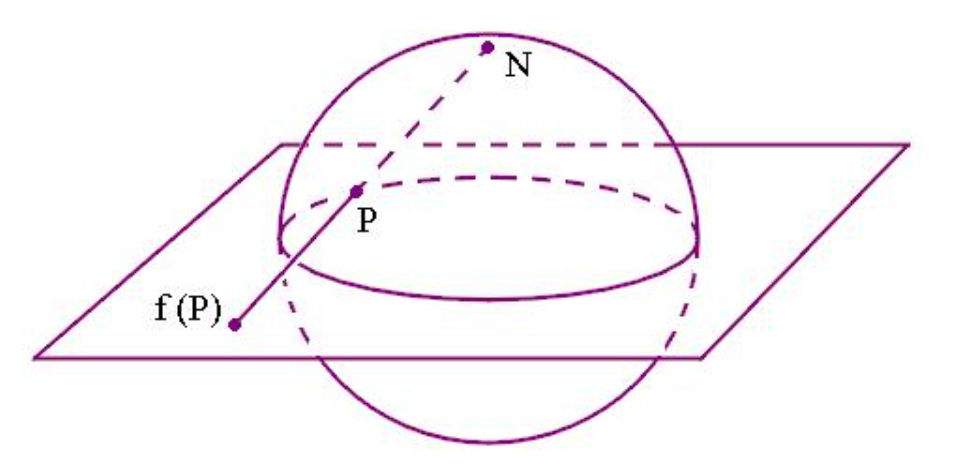
proof. Let $N = (0,\dots,0,1)$ be the north pole and $S=(0,\dots,0,-1)$ the south pole of $S^n$. Define a mapping $\pi_1: S^n -{N} \to \mathbb R^n$ that takes $p=(x_1,\dots,x_{n+1})$ in $S^n - {N}$ into the intersection of the hyperplane $x_{n+1} = 0$ with the line that passes through $p$ and $N$. That is, \(\pi_1(x_1, \dots,x_{n+1}) = (\frac{x_1}{1-x_{n+1}}, \dots,\frac{x_{n}}{1-x_{n+1}})\) The map $\pi_1$ is a differentiable, injective and surjective. Similarly, the stereographic projection $\pi_2: S^n -{S} \to \mathbb R^n$ has the same properties. \(\pi_2(x_1, \dots,x_{n+1}) = (\frac{x_1}{1+x_{n+1}}, \dots,\frac{x_{n}}{1+x_{n+1}})\) These two parametrization cover $S^n$. If we denote $(y_1, \dots, y_n) = \pi_1$ and $(y_1’, \dots, y_n’) = \pi_2$, then we have \(\pi_2 \circ \pi_1^{-1}:\mathbb R^n -\{0\} \to \mathbb R^n -\{0\};(y_1,\dots,y_n) \mapsto(\frac{y_1}{\sum_{i=1}^{n}y_i^2}, \dots, \frac{y_n}{\sum_{i=1}^{n}y_i^2})\) Thus, ${(\mathbb R^n, \pi_1^{-1}),(\mathbb R^n,\pi_2^{-1})}$ is a differentiable structure on $S^n$. Obviously, $\pi_1^{-1}(\mathbb R^n) \cap \pi_2^{-1}(\mathbb R^n) = S^n - {N \cup S}$ is connected, thus $S^n$ is orientable.

Example. preserve or reserve the orientation Let $A:S^n \to S^n; p \mapsto -p$. $A$ is differentible and $A^2 = \mathrm{id}$. $A$ reserves the orientation if $n$ is even, $A$ preserves the orientation if $n$ is odd.

Discontinuous action of a group

projective space

上次课，我们看到了射影平面的一种构造方法，现在我们还可以利用这个映射$A$去从另外一个角度来构造射影平面。 我们注意到，每一条穿过原点的直线，事实上都对应着$S^n$上的一对对径点 $p$ 和 $-p$。由此我们试着给$P^n$一个新的微分结构刻画。 For this, we first introduce on $S^n \subset \mathbb R^{n+1}$ a differentible structure of a regular suface \(x_i^+:U_i \to S^n;(x_1,\dots,x_{i-1},x_{i+1},\dots,x_{n+1}) \to (x_1,\dots,x_{i-1},D_i,x_{i+1},\dots,x_{n+1})\) \(x_i^-:U_i \to S^n;(x_1,\dots,x_{i-1},x_{i+1},\dots,x_{n+1}) \to (x_1,\dots,x_{i-1},-D_i,x_{i+1},\dots,x_{n+1})\) \(D_i=\sqrt{1-(x_1^2+\cdots+x_{i-1}^2+x_{i+1}^2+\cdots+x_{n+1}^2)}\) \(U_i = \left\{(x1,\dots,x_{n+1}):x_i=0,\sum_{i=1}^{n+1}x^2_i\right\}\) We can verify that these parametrization satisfied the conditions of regular suface. Therefore, the family \(\{(U_i,x_i^+),(U_i,x_i^-)\}, i=1,\dots,n+1\)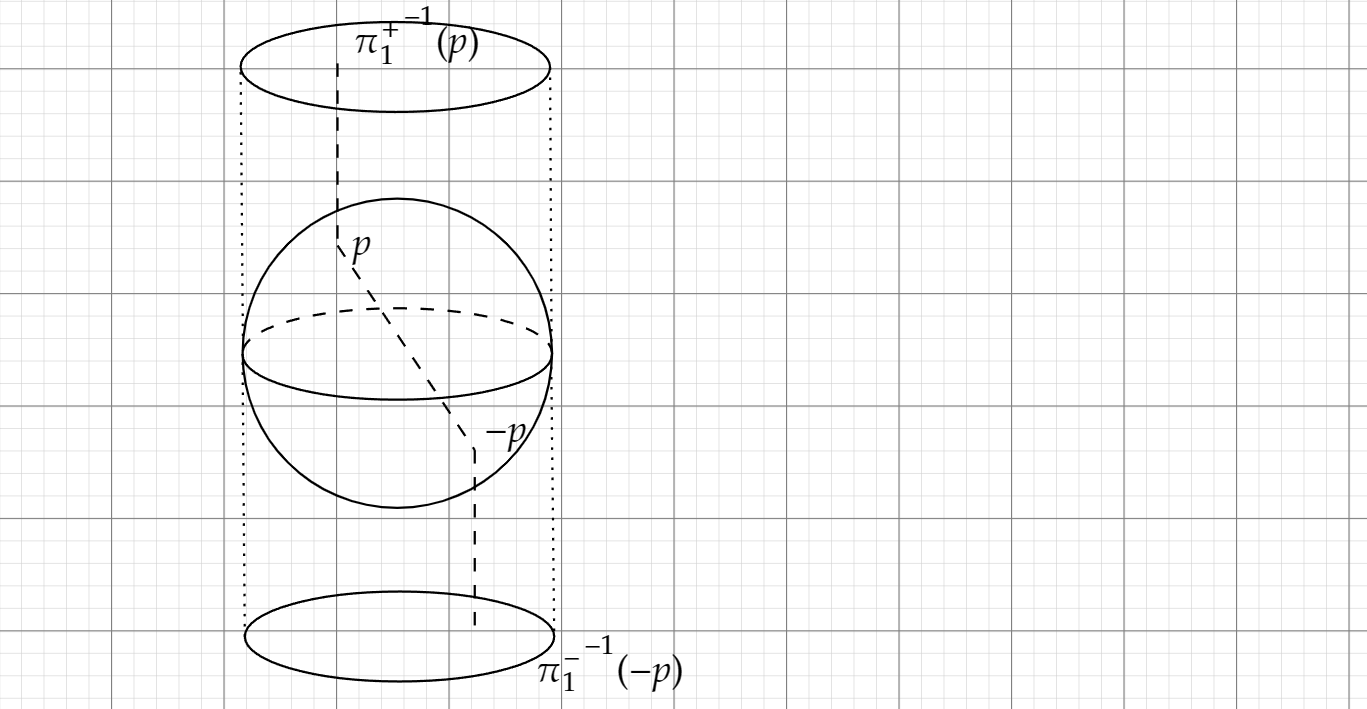

Now, we start to construct the canonical projection $\pi:S^n \to P^n(\mathbb R); p \to {p,-p}$（即将对径点粘在一起视作一个等价类） Then, we have $\pi \circ x_i^+ = \pi \circ x_i^-$. we are going to define a mapping \(y_i:U_i \to P^n(\mathbb R);q \to\pi \circ x^+_i(q)\) Since $\pi$ restricted to $x_i^+(U_i)$ is one-to-one corresponding, we have \(y^{-1}_i \circ y_j^{-1} = (\pi\circ x_i^+)^{-1} \circ (\pi\circ x_j^+)= (x_i^+)^{-1} \circ x_j^+\) which yields the differentiability of $y_i^{-1} \circ y_j$. Thus, ${y_i}$ is a differentiabe structure of $P^n(\mathbb R^n)$. \((\frac{x_1}{x_i},\dots,\frac{x_{i-1}}{x_i},1,\frac{x_{i+1}}{x_i},\dots,\frac{x_{n+1}}{x_i}) \leftrightarrow(x_1,\dots,x_{i-1},D_i,x_{i+1},\dots,x_{n+1})\)

Discontinuous action of a group

事实上，从上一个例子的构造方法，我们可以抽象出一种利用已有流形以及流形上的一个自同构子群去构造新的流形的方法。

Def. $G$ acts on differentiable manifold $M$ If there exist a mapping $\varphi:G \times M \to M$ such that: (i) For each $g \in G$, the mapping $\varphi_g:M \to M$ given by $\varphi_g(p) = \varphi (g,p), p \in M$, is a diffeomorphism, and $\varphi_e = \mathrm{id}$. (ii) If $g_1,g_2 \in G, \varphi {g_1 g_2} = \varphi{g_1} \circ \varphi_{g_2}$.

We said the action is properly discontinuous if every $p \in M$ has a neighborhood $U \subset M$ such that $U \cap g(U) = \emptyset$ for all $g \not = e$. 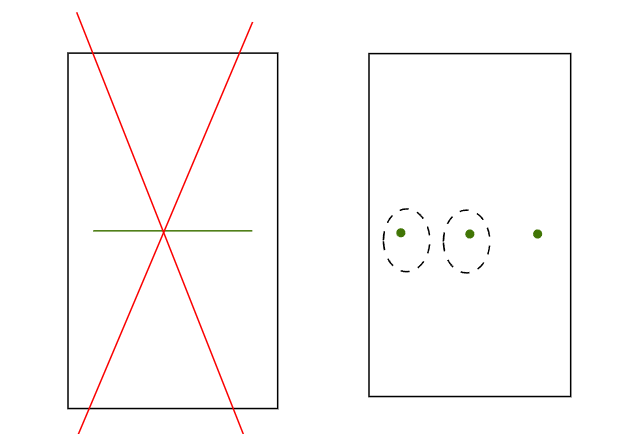When $G$ acts on $M$, the action determined an equivalence relation $\sim$ on $M$: \(p_1 \sim p_2 \Leftrightarrow p_2 = g p_1\text{ for some } g \in G\) Denote the quotient space of $M$ as $M/G = M/\sim$, and define a mapping \(\pi:M \to M/G;p\mapsto [p] = Gp\) we called it the projection of $M$ onto $M/G$.

Examples

Torus $M = \mathbb R^2$, $G=\mathbb Z^2$ Klein bottle Mobius band

Tangent field

接下来，我们需要谈论“连续的微分”。但是，按照我们之前的定义，不同点之间的切空间互相独立，完全没有办法说明白什么样子的微分是“连续的”，什么样的微分是“有断层的”。为此我们需要引入一些新的结构来说明“微分变化不大”是什么意思。

The tangent bundles

Let $M^n$ be a diferentiable manifold and let $TM = {(p,v):p\in M, v \in T_pM}$. 这看上去就像是将切空间都装在一起，但是现在这个集合看上去很松散，所以我们需要去构造一个合适的拓扑去约束这个结构。 We are going to provide the set $TM$ with a differentiable structure on it, which called tangen bundles of $M$. 事实上，我们在原有的流形上已经存在了一个微分结构，所以，我们比较自然的想法便是立足于这个原有的微分结构，然后进行适当的拓展，使得这个微分结构可以cover住多出来的切空间部分。 Let ${(U_\alpha, \mathbf x_\alpha)}$ be a maximal differentiable structure on $M$. Denote $(x_1^\alpha,\dots,x_n^\alpha)$ the coordinates of $U_\alpha$ and ${\frac{\partial }{\partial x_1}, \dots, \frac{\partial }{\partial x_n}}$ the associated bases to the tangent spaces of $\mathbf x \alpha(U\alpha)$. For every $\alpha$, we define \(\mathbf y_\alpha:U_\alpha \times \mathbb R^n \to TM; (x_1^\alpha,\dots,x_n^\alpha, u_1,\dots,u_n) \mapsto (\mathbf x_\alpha, \sum_{i=1}^{n} u_i \frac{\partial }{\partial x_i})\) 事实上，我们这里使用的方法，正是利用流形每个局部都微分同胚于某个欧氏空间的一部分的特性，从而将欧氏空间中的“连续微分”的概念搬运到流形上面，但现在，我们还需要证明这样的定义在不同的参数化之间也是契合的。 We are going to show that ${(U_\alpha \times \mathbb R^n,\mathbf y_\alpha)}$ is a differentiable structure on $TM$. For (1), \(\bigcup_\alpha \mathbf x_\alpha(U_\alpha) = M,(d \mathbf x_\alpha)_q(\mathbb R^n) = T_{\mathbf x_\alpha(q)}M \Rightarrow \bigcup_\alpha \mathbf y_\alpha(U_\alpha \times \mathbb R^n) = TM\) For (2), let \((p,v) \in \mathbf y_\alpha (U_\alpha \times \mathbb R^n)\cap \mathbf y_\beta (U_\beta \times \mathbb R^n)\) Then, we can write \((p,v) = (\mathbf x_\alpha(q_\alpha),d\mathbf x_\alpha(v_\alpha)) = (\mathbf x_\beta(q_\beta),d\mathbf x_\beta(v_\beta))\) Therefore, \(\mathbf y_\beta^{-1} \circ \mathbf y_\alpha(q_\alpha,v_\alpha) = (\mathbf x_\beta^{-1} \circ \mathbf x_\alpha (q_\alpha), d(\mathbf x_\beta^{-1} \circ \mathbf x_\alpha)(v_\alpha))\) Then, $\mathbf y_\beta^{-1} \circ \mathbf y_\alpha$ is differentiable because of the differentiability of $\mathbf x_\beta^{-1} \circ \mathbf x_\alpha$.

Tengent field

bracket

Two way to consider bracket

Others

Topology of manifold

differentiable partition of unity