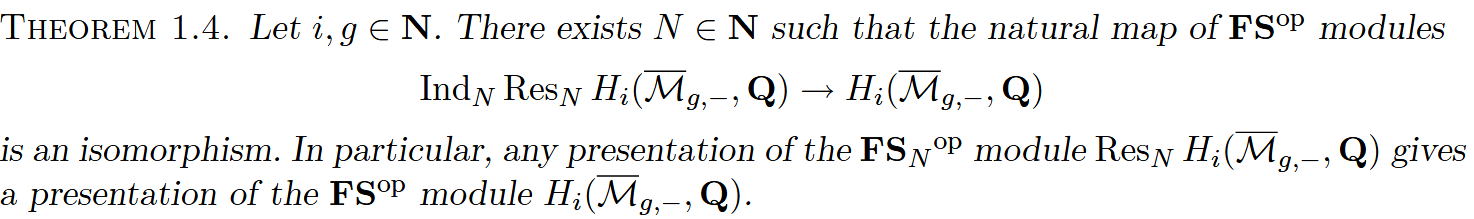Limit, stability and representation: From Limit of homology groups to Representation Stability
Published:
Homological stability
Definition 1.3.
A sequence of spaces or groups with maps
\[X_{0}\xrightarrow{s_{0}}\ldots\xrightarrow{s_{n-2}}X_{n-1}\xrightarrow{s_{n-1}}X_{n}\xrightarrow{s_{n}}X_{n+1}\xrightarrow{s_{n+1}}\ldots\]satisfies homological stability if, for each $k$, the induced map in degree-$k$ homology
\[(s_{n})_{*}:H_{k}(X_{n};\mathbb{Z}) \to H_{k}(X_{n+1};\mathbb{Z})\]is an isomorphism for all $𝑛 ≥ 𝑁_𝑘$ for some stability threshold $𝑁_𝑘 \in \mathbb Z$ depending on $k$.
Example.
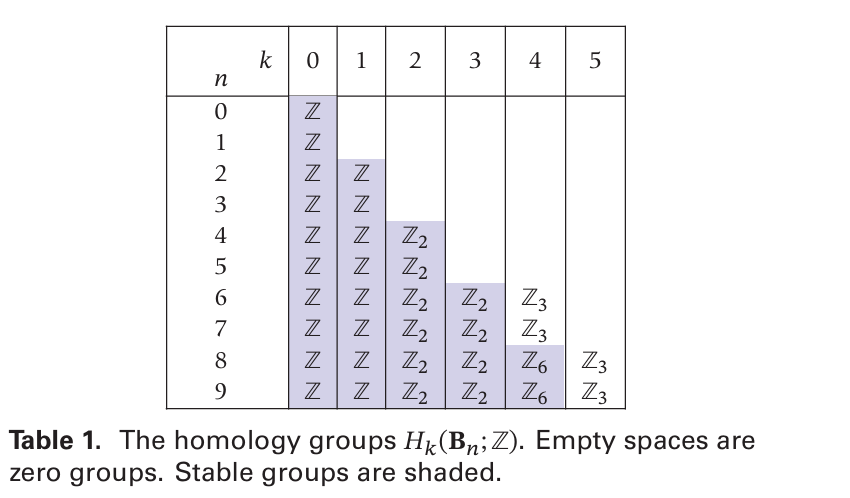
似乎没必要去细讲$F_n(M)$ 和 $C_n(M)$
Definition: group homology and group cohomology
For a group G,
• The group homology of G with coefficients in an abelian group A is defined as:
\[H_*(G; A) := H_*(BG; A)\]• The group cohomology of G with coefficients in an abelian group A is defined as:
\[H^*(G; A) := H^*(BG; A)\]Here, EG is a contractible space on which G acts freely, and BG = EG/G is the classifying space of G.
$BG$ is unique up to (weak) homotopy equivalence.
If $G$ is a discrete group, then $BG$ is precisely an Eilenberg-MacLane space $K(G,1)$.
Eilenberg-MacLane space


Proposition.
For $A$ a countable abelian group, is an Eilenberg-MacLane space,
\[\pi_q(A[\mathbb S^n]) = \begin{cases}A & n=q\\*&n\not = q\end{cases}\]
Definition 2.1.
Let $M$ be a topological space, such as a graph or a manifold.
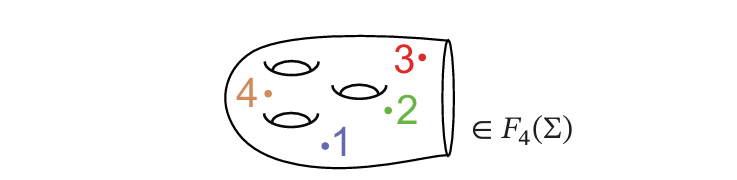
The (ordered) configuration space $F_n(M)$ of $n$ particles on $M$ is the space
\[F_n(M) = \set{(x_1, ..., x_n) \in M^n \mid x_1, ..., x_n \text{ distinct}},\]topologized as a subspace of $M^n$ .
Notably, $F_0(M)$ is a point and $F_1(M) = M$ .
Theorem 2.4 (McDuff [McD75]; Segal [Seg79]).
Let $M$ be the interior of a compact connected manifold with nonempty boundary.
For each $k ≥ 0$ the maps
\[(s_{n})_{*}: H_{k}(C_{n}(M); \mathbb{Z}) \rightarrow H_{k}(C_{n+1}(M); \mathbb{Z})\]are isomorphisms for $n ≥ 2k$.
homological stability(Quillen’s arguement)
[Hatcher, A., & Wahl, N. (2010). Stabilization for mapping class groups of 3-manifolds. Duke Mathematical Journal, 155(2), 205–269. https://doi.org/10.1215/00127094-2010-055]
Thm. Quillen’s arguement for homological stability
Let $0 \hookrightarrow G_1 \hookrightarrow G_2 \hookrightarrow G_3 \hookrightarrow \cdots \hookrightarrow G_n \hookrightarrow \cdots$ be a sequence of discrete groups.
For each $n$, let $W_n$ be a simplicial complex with a simplicial action of $G_n$ with
- $W_n$ is $\lfloor \frac{n-2}{2}\rfloor$-connected
- $\forall p > 0$, $G_n$ act transitively on the set of $p$-simplices.
$\forall \sigma_p$ in $W_n$, we have ${g \in G_n: g {\sigma_p} = Id{\sigma_p}} = \mathrm{stab}(\sigma_p):={g \in G_n:g\sigma_p = \sigma_p}$ - $\exists h \in G_n$ s.t. $h^{-1}\mathrm{stab}(\sigma_p)h = G_{n-p-1}$
$\forall$ edge $[v_0,v_1]$ in $W_n$, there exist $g \in G$ s.t. $g v_0 = v_1$ and for all $h\in G$ if $h {[v_0,v_1]} = Id{[v_0,v_1]}$ then $gh=hg$.
Then, the sequence ${G_n}_n$ is homologically stable.
Specifically, $H_k(G_n) \to H_k(G_{n+1})$ is isomorphism for $n \le 2k+1$ and a surjection for $n = 2k+1$.
Example. arc conplex [ hatcher and waul ]

对于流形 $M$ 的有序配置空间 $F_n(M)$,经典同调稳定性不成立:
\[H_1(F_n(M); \mathbb{Z}) \sim n^2 \quad (n \to \infty)\]表示稳定性的提出
- Church 与 Farb 提出:尽管同调作为 Abel 群序列不稳定,但作为 $S_n$-表示序列是稳定的。
- $S_n$ 作用在 $F_n(M)$ 上,诱导其(上)同调上的表示结构。
Young graph
$S_n$表示分解与杨图
$S_n$ is finite group, then $V$ is semi-simple.
Consider the irreducible rational $S_n$-representation.
每一个不可约表示都和一个杨图一一对应。
考虑$n$的一个划分$\lambda$和对应的杨图$T_\lambda$,那么记

如此,便可以给出$\lambda$对应的表示$V_\lambda= \mathbb C[G]c_\lambda$.
考虑$S_n$在$F_n(\mathbb C)$上的作用,那么我们可以诱导出$S_n$在$H_k(F_n(\mathbb C),\mathbb Q)$上的作用
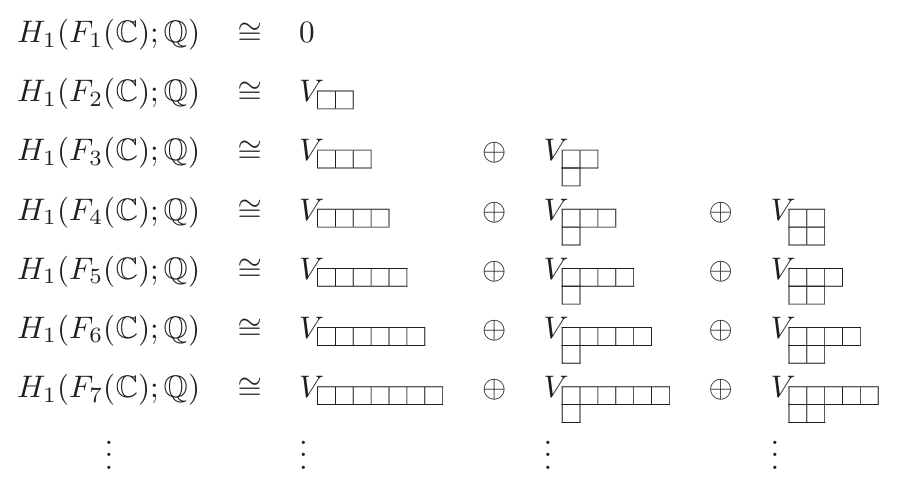
当$n \ge 4k$时,$H_{n-1}$到$H_{n}$不再增加新的部分,而是在每一个部分第一行的右侧继续添加方块。
随后,Church证明了$H^k(F_n(M);\mathbb Q)$也存在类似的,甚至不一定是$F_n(M)$还有一系列的其他空间也有类似的性质与稳定性。
FI-module
FI-module $V$ over $R$
F finite; I injective.
Definition5.2.
Let 𝖥𝖨 be the category whose objects are finite sets (including$\emptyset$), and whose morphisms are all injective maps.
Given a commutative ring $R$ (typically ℤ or ℚ), an 𝖥𝖨-module 𝑉 over $R$ is a functor from 𝖥𝖨 to the category of $R$-modules.
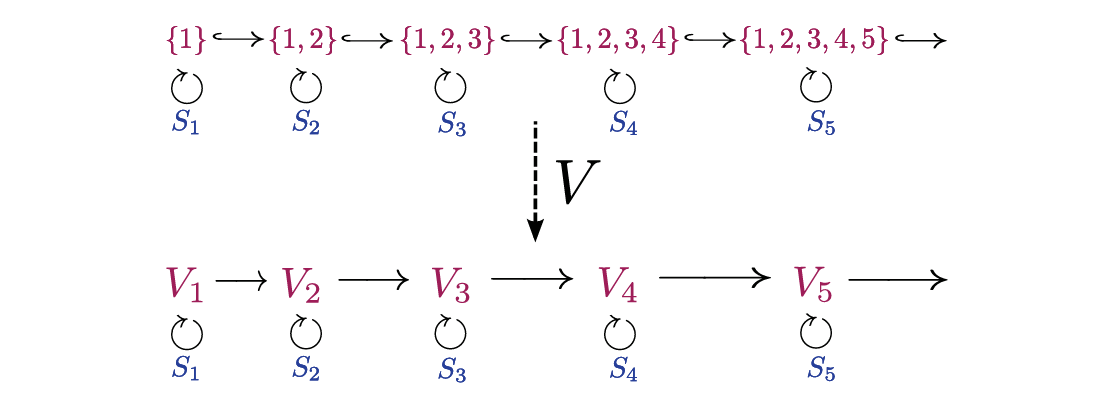
$V_n \to V_{n+1}$ induced by $[n] \hookrightarrow [n+1]$.
Example.

counterexasmple.

Representation stability
Character polynomials.
We finish this section by proving a refined version of Theorem 1.5.
Recall that for each $i \geq 1$ and any $n \geq 0$, the class function $X_i: S_n \to \mathbb{N}$ is defined by
\[[ X_i(\sigma) := \text{number of } i\text{-cycles in } \sigma. ]\]For example, $X_1(\sigma)$ is the number of fixed points of the permutation $\sigma$.
Polynomials in the variables $X_i$ are called character polynomials.
Class functions form a ring under pointwise product, so any character polynomial $P \in \mathbb{Q}[X_1, X_2, \ldots]$ also defines a class function $P: S_n \to \mathbb{Q}$ for all $n \geq 0$.
The degree of a character polynomial is defined by setting $\deg(X_i) = i$.
Theorem 3.3.4 (Polynomiality of characters).
Let $V$ be a finitely generated FI-module over a field of characteristic $0$.
There is a unique polynomial $P_V \in \mathbb{Q}[X_1, X_2, \ldots]$ with $\deg P_V \leq \operatorname{weight}(V)$ such that for all $n \geq \operatorname{stab-deg}(V) + \operatorname{weight}(V)$ and all $\sigma \in S_n$ ,
\[\chi_{V_n}(\sigma) = P_V(\sigma).\]Theorem 5.4 (Church-Ellenberg-Farb [CEF15]).
Let $V$ be an FI-module over $\mathbb Q$, finitely generated in degree $≤ d$. The following hold.
Finite generation. For $n ≥ d$,
\[S_{n+1} · t_n(V_n) \text{ spans } V_{n+1}.\]- Multiplicity stability. For all $n ≥ 2d$ the decomposition of $V_n$ into irreducible constituents stabilizes.
- Character polynomials. The character of $V_n$ is independent of n for all $n ≥ 2d$.
furthermore(时间够再提,时间不够就算了)
Deligne-Mumford compactication
1.1 稳定曲线 (Stable Curves)
Definition 3.1.
Let $C$ be an algebraic curve over an algebraically closed field $k$. We say that $C$ is semi-stable if it is reduced, and if its singular points are ordinary double points.
We say that $C$ is stable if, moreover, the following conditions are verified: (1) $C$ is connected and projective, of arithmetic genus $p_a(C) \geq 2$ . (2) Let $\Gamma$ be an irreducible component of $C$ that is isomorphic to $\mathbb{P}^1_k$ . Then it intersects the other irreducible components at at least three points.
Properties:
- 自同构群有限
- 构成模空间 $\overline{M}_{g,n}$ 的点的几何对象
- 允许节点和标记点,用于紧化模空间
Def2 [Deligne-Mumford]
The points in the boundary of the moduli spaces of pointed, nodal curves with finite automorphism group.
These curves are called stable curves (or pointed stable curves).
THEOREM 1.2. [Tosteson, P. (2021). Stability in the homology of Deligne–Mumford compactifications. Compositio Mathematica, 157(12), 2635–2656. doi:10.1112/S0010437X21007582]
Let $g, i \in \mathbf{N}$. Then the $\mathbf{FS}^{\mathrm{op}}$ module
\[n \mapsto H_i(\overline{\mathcal{M}}_{g,n}, \mathbf{Q})\]is a subquotient of an extension of $\mathbf{FS}^{\mathrm{op}}$ modules that are finitely generated in degree $\leq 8g^2i^2 + 29g^2i + 16gi^2 + 21g^2 + 10gi - 6g$.